
Zadanie Pakowanie kontenerów (pak)
Pomóż nam usprawnić bazę zadań!
Pakowanie kontenerów
Limit pamięci: 32 MB
Pewna fabryka pakuje swoje wyroby do pudełek, które mają kształt walca.
Podstawy wszystkich pudełek są takie same.
Wysokość każdego pudełka jest zawsze nieujemną, całkowitą potęgą dwójki, tzn. liczbą postaci 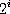 , dla pewnego
, dla pewnego 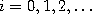 .
Liczbę
.
Liczbę 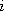 (wykładnik potęgi), która charakteryzuje wielkość pudełka, nazywamy rozmiarem tego pudełka.
We wszystkich pudełkach znajduje się taki sam towar, ale w różnych pudełkach wartość towaru może być różna — towar wyprodukowany wcześniej jest tańszy.
Dyrekcja fabryki wydała zarządzenie, żeby starać się wydawać najpierw towar najstarszy, czyli o najmniejszej wartości.
Towar jest wywożony z magazynu w kontenerach.
Każdy kontener, podobnie jak pudełka, ma kształt walca.
Średnica kontenera jest niewiele większa od średnicy pudełek tak, że pudełka można swobodnie umieszczać w kontenerach.
Wysokość każdego kontenera jest też nieujemną, całkowitą potęgą dwójki.
Podobnie jak w przypadku pudełek, rozmiarem kontenera nazywamy wykładnik tej potęgi.
Żeby bezpiecznie przewozić towar w kontenerze, należy go szczelnie wypełnić pudełkami,
tzn. suma wysokości umieszczonych w kontenerze pudełek musi być równa wysokości tego kontenera.
(wykładnik potęgi), która charakteryzuje wielkość pudełka, nazywamy rozmiarem tego pudełka.
We wszystkich pudełkach znajduje się taki sam towar, ale w różnych pudełkach wartość towaru może być różna — towar wyprodukowany wcześniej jest tańszy.
Dyrekcja fabryki wydała zarządzenie, żeby starać się wydawać najpierw towar najstarszy, czyli o najmniejszej wartości.
Towar jest wywożony z magazynu w kontenerach.
Każdy kontener, podobnie jak pudełka, ma kształt walca.
Średnica kontenera jest niewiele większa od średnicy pudełek tak, że pudełka można swobodnie umieszczać w kontenerach.
Wysokość każdego kontenera jest też nieujemną, całkowitą potęgą dwójki.
Podobnie jak w przypadku pudełek, rozmiarem kontenera nazywamy wykładnik tej potęgi.
Żeby bezpiecznie przewozić towar w kontenerze, należy go szczelnie wypełnić pudełkami,
tzn. suma wysokości umieszczonych w kontenerze pudełek musi być równa wysokości tego kontenera.
Do magazynu dostarczono zestaw kontenerów. Sprawdź, czy można pudełkami z magazynu wypełnić szczelnie wszystkie kontenery. Jeśli tak, to podaj minimalną wartość towaru jaki można wywieźć z magazynu w tych, szczelnie wypełnionych, kontenerach.
Przykład
Rozważmy magazyn, w którym znajduje się 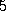 pudełek o następujących rozmiarach i wartościach przechowywanego w nich towaru:
pudełek o następujących rozmiarach i wartościach przechowywanego w nich towaru:
1 3 1 2 3 5 2 1 1 4
Dwa kontenery o rozmiarach 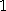 i
i 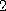 można szczelnie wypełnić dwoma pudełkami o łącznej wartości
można szczelnie wypełnić dwoma pudełkami o łącznej wartości 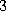 ,
,  lub
lub 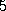 ,
lub trzema pudełkami o łącznej wartości
,
lub trzema pudełkami o łącznej wartości 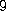 .
Kontener o rozmiarze
.
Kontener o rozmiarze 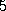 nie da się szczelnie wypełnić pudełkami z magazynu.
nie da się szczelnie wypełnić pudełkami z magazynu.
Zadanie
Napisz program, który:
- wczytuje ze standardowego wejścia charakterystyki pudełek w magazynie (rozmiar, wartość) oraz charakterystyki kontenerów (ile jest kontenerów danego rozmiaru);
- sprawdza, czy wszystkie kontenery w zestawie można szczelnie wypełnić pudełkami z magazynu, a jeśli tak, to oblicza minimalną wartość towaru jaką można w tych kontenerach wywieźć z magazynu;
- zapisuje wynik na standardowe wyjście.
Wejście
W pierwszym wierszu standardowego wejścia znajduje się liczba całkowita  ,
, 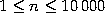 .
Jest to liczba pudełek w magazynie.
W każdym z
.
Jest to liczba pudełek w magazynie.
W każdym z  kolejnych wierszy zapisane są dwie nieujemne liczby całkowite oddzielone pojedynczym odstępem.
Są to charakterystyki jednego pudełka, odpowiednio, rozmiar pudełka i wartość zawartego w nim towaru.
Rozmiar pudełka jest nie większy od
kolejnych wierszy zapisane są dwie nieujemne liczby całkowite oddzielone pojedynczym odstępem.
Są to charakterystyki jednego pudełka, odpowiednio, rozmiar pudełka i wartość zawartego w nim towaru.
Rozmiar pudełka jest nie większy od 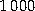 , natomiast wartość jest nie większa od
, natomiast wartość jest nie większa od 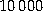 .
.
W kolejnym wierszu podana jest dodatnia liczba całkowita 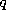 określająca, ile różnych rozmiarów mają kontenery dostarczone do magazynu.
W każdym z kolejnych
określająca, ile różnych rozmiarów mają kontenery dostarczone do magazynu.
W każdym z kolejnych 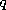 wierszy jest zapisana para dodatnich liczb całkowitych oddzielonych pojedynczym odstępem.
Pierwsza z tych liczb jest rozmiarem kontenera, natomiast druga jest liczbą dostarczonych kontenerów o tym rozmiarze.
Wiadomo, że maksymalna liczba kontenerów nie przekracza
wierszy jest zapisana para dodatnich liczb całkowitych oddzielonych pojedynczym odstępem.
Pierwsza z tych liczb jest rozmiarem kontenera, natomiast druga jest liczbą dostarczonych kontenerów o tym rozmiarze.
Wiadomo, że maksymalna liczba kontenerów nie przekracza 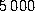 , a rozmiar kontenera jest nie większy od
, a rozmiar kontenera jest nie większy od 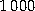 .
.
Wyjście
Twój program powinien zapisać w pierwszym i jedynym wierszu standardowego wyjścia:
- jedno słowo NIE, jeżeli nie da się szczelnie wypełnić pudełkami z magazynu kontenerów z podanego zestawu, lub
- jedną liczbę całkowitą, której wartość jest równa minimalnej, łącznej wartości towaru z pudełek, którymi można szczelnie wypełnić wszystkie kontenery z podanego zestawu.
Przykład
Dla danych wejściowych:
5 1 3 1 2 3 5 2 1 1 4 2 1 1 2 1
poprawną odpowiedzią jest:
3
Autor zadania: Wojciech Rytter.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English